PID Control For A Planar Aquatic Vehicle in Point Vortex Flows

In this project, I developed a dynamic model for a novel fluid-propulsive aquatic vehicle in an ideal fluid that exerts control over its motion using impulsive fluid-ejection events. The control input for the system is modeled as an instantaneous placement of a pair of symmetrically located counter-rotating point vortices. A snapshot of a simulation for this system after shedding some number of directed vortex pairs is shown below.

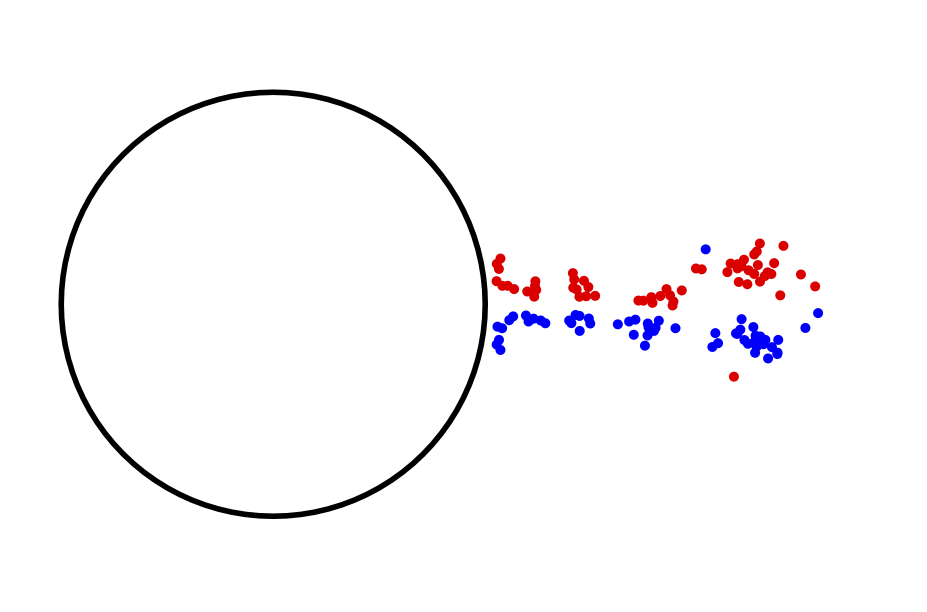
$$\text{Fig. 1. A fluid-propulsive aquatic vehicle that locomotes using impulsive fluid-ejection events.}$$

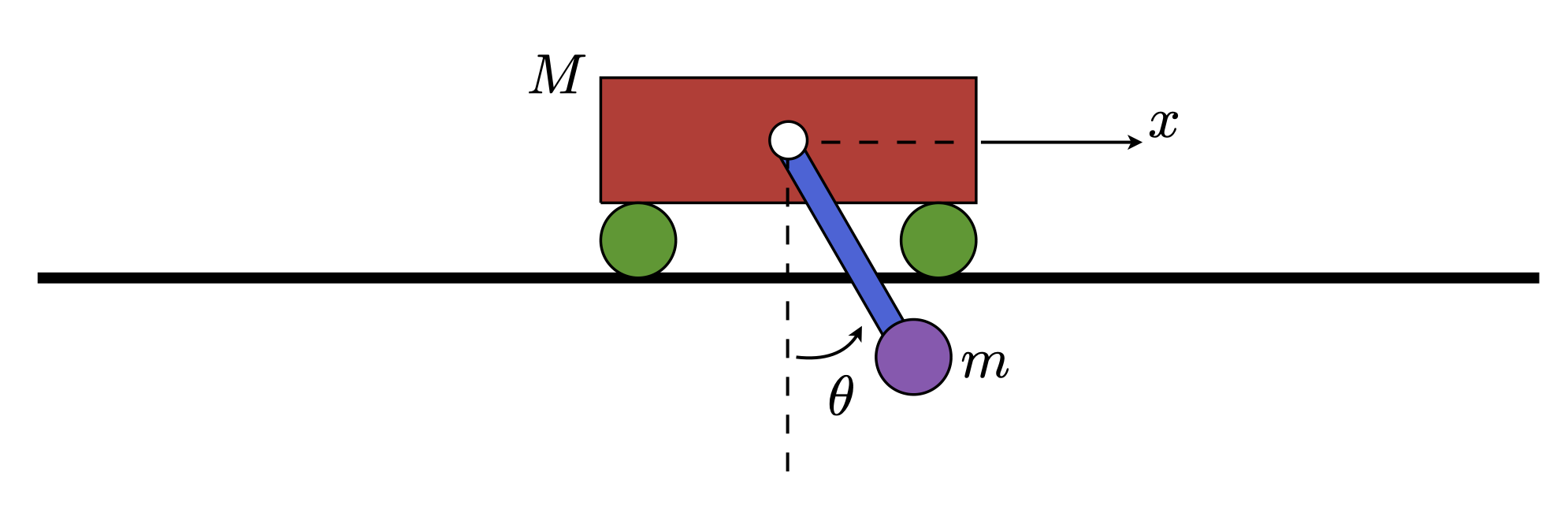
A free-body diagram of the system can be seen below.

Dynamics

For the full dynamics of the system, see my thesis. For brevity, assume hybrid dynamics of the form

$$ \ddot{q} = f(q,\dot{q}),$$

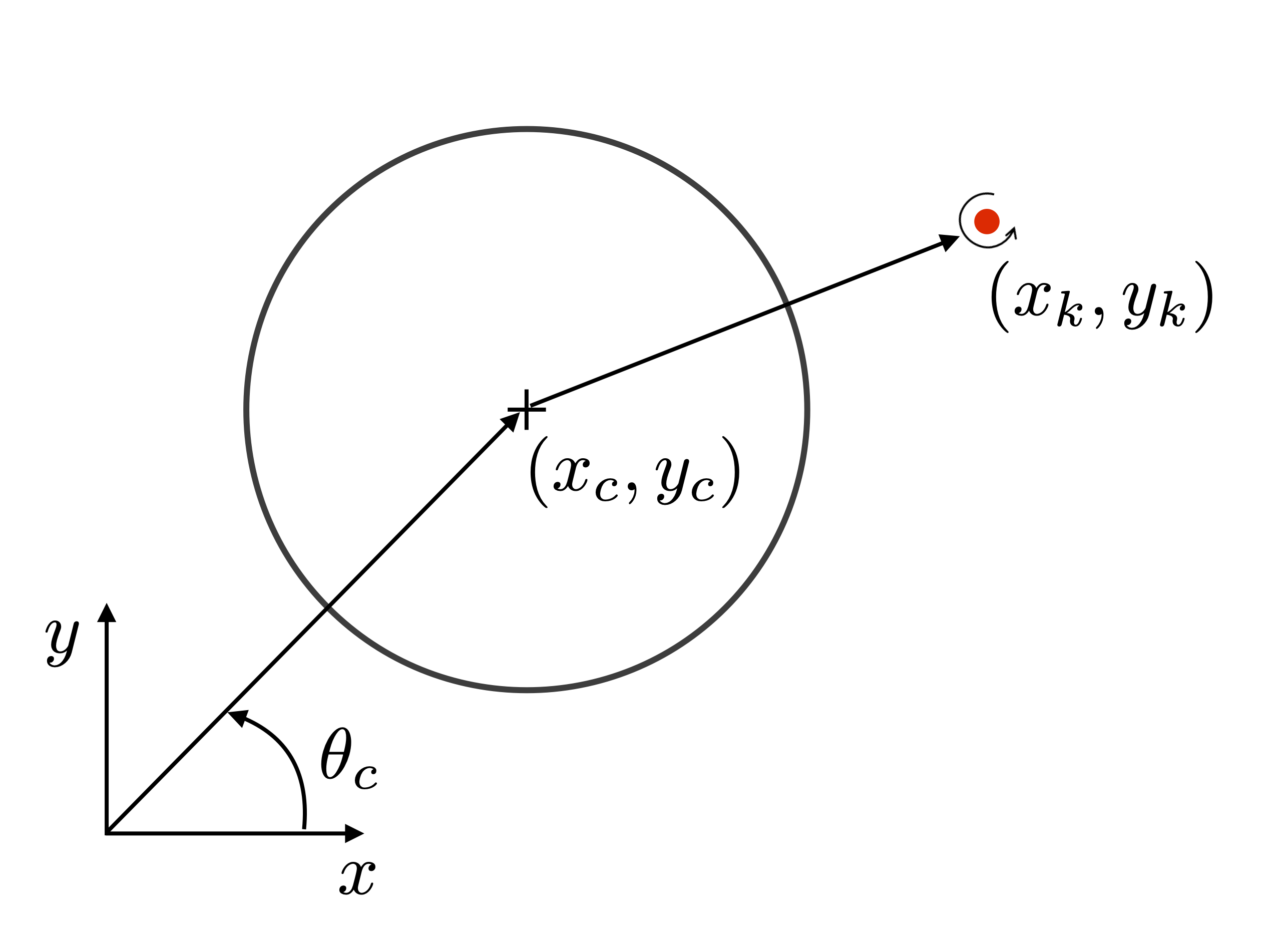
where \(q = (q_c, \dot{q}_c, q_v)^\top\). We designate \(q_c = (x_c, \; y_c, \; \theta_c)^\top \in \text{SE}(2)\) as the position and orientation of the aquatic vehicle, \(q_v = (x_c+x_k,\; y_c + y_k, \; \cdots, \; x_c + x_N, \; y_c + y_N)^\top\) be the positions of the vortices in the inertial frame, where each pair \((x_k, \; y_k)\in \mathbb{R}^2\) is written in the body frame of the cylinder.

Along with \(\ddot{q}\), we consider the impulsive equation

$$q(t_j^+) = C_jq(t_j^-) + D_jv_j.$$

The notation \(()^-\) and \(()^+\) denote the time before and after an impulsive control input \(v_j\) is applied. Matrices \(C_j\) and \(D_j\) ensure that only the state variables affected at time \(t=t_j\) by the impulse are updated. The control input is given by

$$\mathbf{v}_j = \begin{bmatrix} \frac{\Gamma_j}{2 \pi} \big ((R + d) + \frac{R^2}{R + d} \big ) \big (\sin(\alpha - \delta \alpha) - \sin(\alpha + \delta \alpha) \big ) \\ \frac{\Gamma_j}{2 \pi} \big ((R + d) + \frac{R^2}{R + d} \big ) \big (\cos(\alpha + \delta \alpha) - \cos(\alpha - \delta \alpha) \big ) \\ \frac{1}{2} \Gamma_j (R + d)^2 \big ( \cos^2(\alpha - \delta \alpha) - \cos^2(\alpha + \delta \alpha) + \sin^2 (\alpha + \delta \alpha) - \sin^2(\alpha - \delta \alpha) \big ) \end{bmatrix}.$$

PID Control

In this work the time between ejection events, \(\Delta t_{j+1} = t_{j+1} - t_j\), is constant. That is, we donot choose when, but at what strength, to eject a vortex pair. Controlling the strength of the vortex pair at each ejection event is accomplished using a standard proportional-derivative control law. Given a setpoint $(x_d,y_d)$, we close the feedback loop on the measured variables $(x_c, y_c)$ and define the error to be

$$\begin{equation} \begin{split} e(t) = & \sqrt{e_x(t)^2 + e_y(t)^2}\\ = & \sqrt{(x_d - x_c)^2 + (y_d - y_c)^2} \end{split} \end{equation}.$$

and let $\Gamma_j(t)$ be equal to the following function.

$$\Gamma_j(t) = K_p e(t) + K_d \frac{d}{dt}e(t) + K_i\int_0^t e(t)dt.$$

Using the proposed control law, we let $x_d = 1, y_d = 1$ to verify its ability to stabilize about the desired setpoint with $K_p = 0.25$, $K_d = 1.15$, and $K_i = 0$. The following figure shows the trajectory of the cylinder with initial conditions $q = 0$ with no initial vortices in the flow.

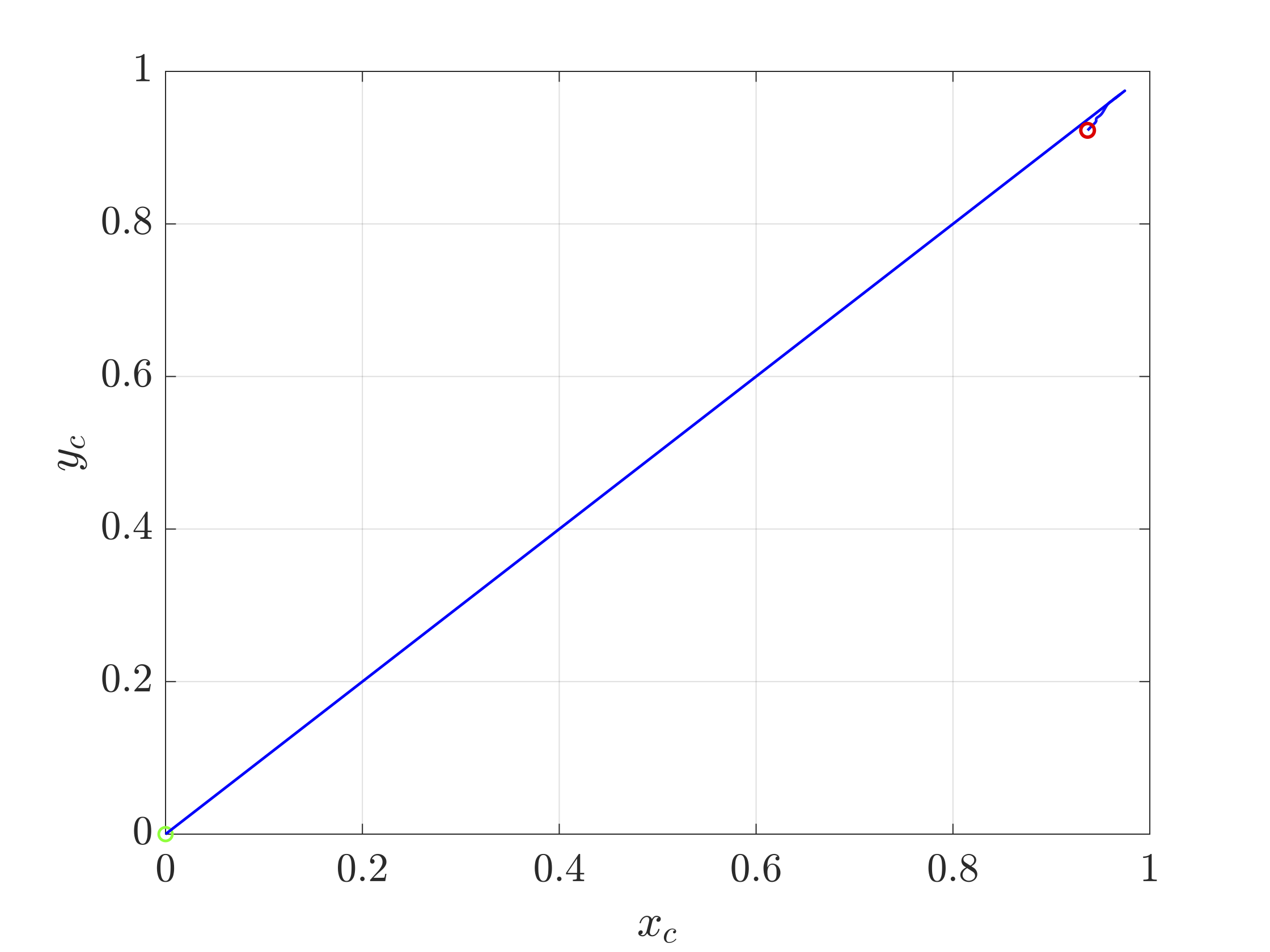
$$\text{Fig. 3. Trajectory of cylinder under a PD control law.}$$

We can see from the above figure that the system stabilizes within some basin of attraction of the setpoint under the PD control law. The following figure shows that the velocity of the cylinder approaches zero as the system approaches the setpoint.

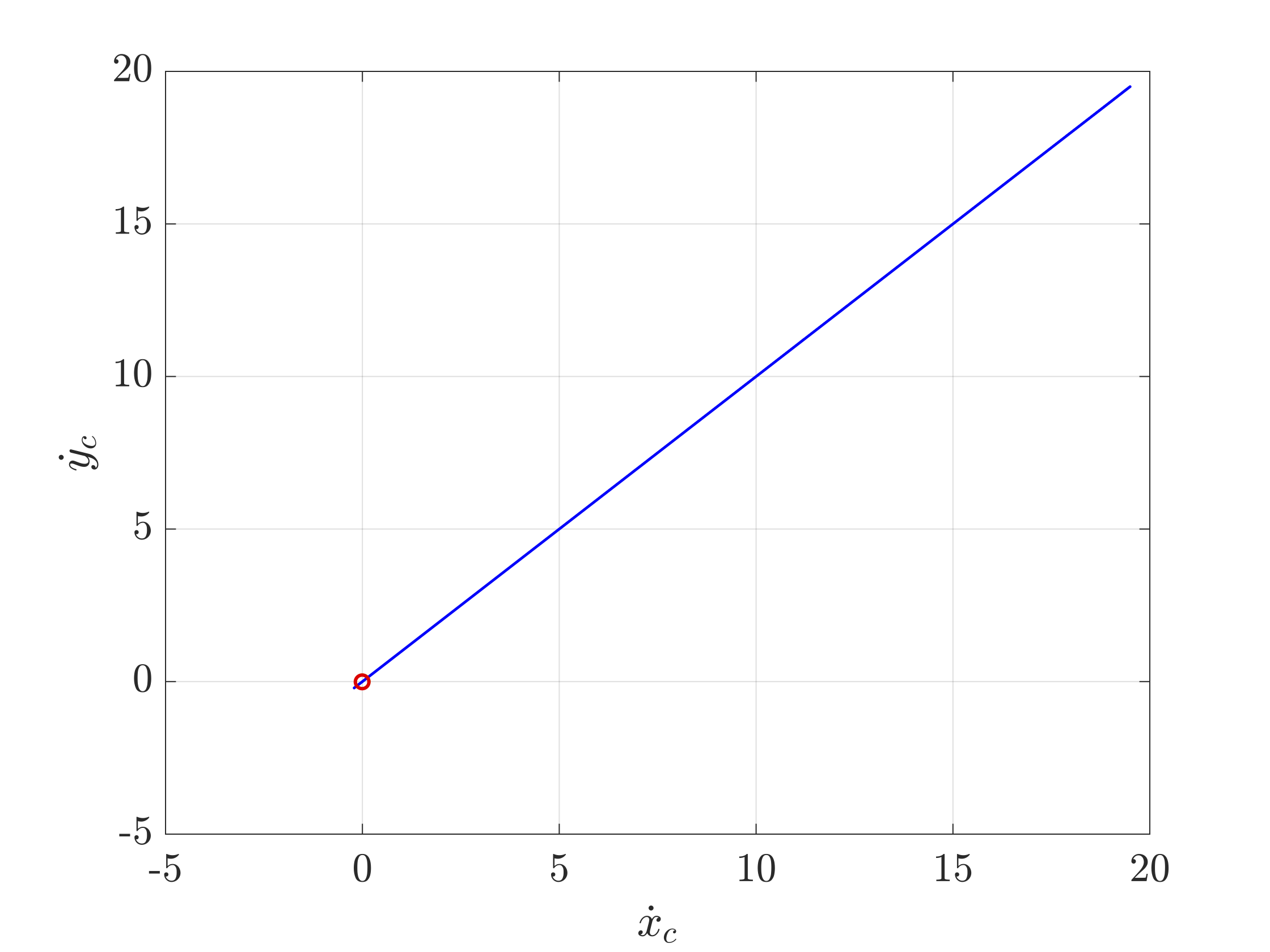
$$\text{Fig. 4. Inertial velocity of the cylinder while controlling to $x_d = 1, y_d = 1$ with initial conditions $q_0 = 0$}.$$

A simulation of the above control law deployed on the aquatic vehicle is shown in the video below. Pay close attention to the initial ejection event. This initial vortex pair is given a lot of strength, and thus separates from the cylinder almost too quickly to notice.